트리 (Tree)
02 Jul 2020 | Data Structure
본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.
Tree
이번 게시물에서 배울 자료구조는 트리(Tree) 입니다. 트리 구조 역시 배열(Array), 연결된 리스트(Linked List)와 동일하게 데이터를 저장하고 데이터간의 Operation을 표현하기 위한 추상화된 데이터 타입 중 하나입니다. 연결된 리스트를 변형한 것으로 연결된 리스트에서는 다른 노드를 가리키는 레퍼런스(Reference)가 하나뿐이었지만, 트리 구조에서는 여러 개의 레퍼런스를 가질 수 있습니다. 한 노드에서 시작해 여러 노드로 뻗어 나가는 모습이 나무를 거꾸로 뒤집은 모양과 유사하다고 하여 트리라는 이름이 붙었습니다.

이미지 출처 : 위키피디아 - 트리(자료구조)
트리 구조는 연결된 리스트의 일부를 변형시킨 것으로 연결된 리스트에서 가능했던 삽입(Insert), 삭제(Delete), 탐색(Search)이 모두 가능합니다. 또한 트리 구조에는 트래버스(Traverse)라는 새로운 작업이 있습니다.
트리 구조에서 사용되는 용어
트리 구조는 연결된 리스트보다는 훨씬 복잡합니다. 그렇기 때문에 트리의 복잡한 구조를 말로 나타내기 위한 다양한 용어들이 존재합니다. 트리 구조에서 사용되는 용어에 대해 아래 그림을 보며 알아봅시다.

이미지 출처 : tutorialspoint.com
가장 먼저 트리 최상단에 위치한 노드를 가리키는 용어는 루트(Root) 입니다. 그리고 직접 연결되어 있는 노드 중 상단에 위치한 노드를 부모(Parent) 노드라고 하고 아래에 위치한 노드를 자식(Child) 노드라고 합니다. 동일한 부모 노드로부터 나온 자식 노드는 서로 형제/자매(Siblings) 노드라고 합니다. 그리고 자식 노드를 갖지 않는 노드는 리프(Leaf) 노드라고 하며 다른 말로는 터미널(Terminal) 노드라고도 합니다. 리프 노드가 아닌 노드는 모두 인터널(Internal) 노드라고 합니다.
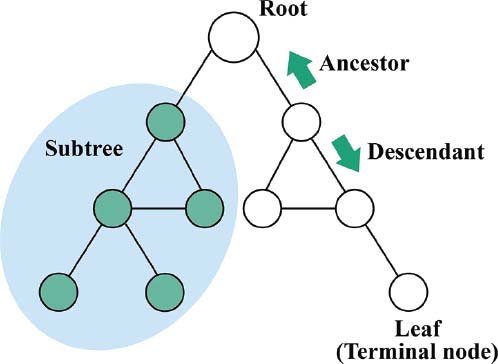
이미지 출처 : science.jrank.org
특정 노드에서부터 트리의 위쪽으로 거슬러 올라가면서 만나는 모든 노드를 조상(Ancestor) 노드라고 하며, 반대로 아래에 있는 모든 노드는 후손(Descendant) 노드라고 합니다.
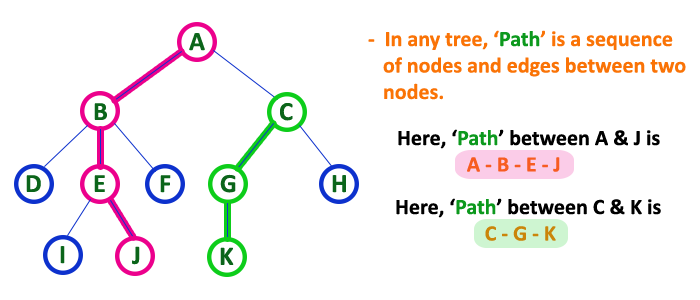
이미지 출처 : btechsmartclass.com
특정 노드로부터 다른 노드로 갈 때 거치는 과정을 경로(Path) 라고 합니다. 경로 길이(Length) 는 출발 노드로부터 목적 노드까지 가는데 거치는 노드의 개수입니다. 위 이미지에서 제시한 두 예시의 경로 길이는 각각 $3, 2$ 가 됩니다. 그리고 깊이(Depth) 는 루트로부터 목적 노드까지의 경로 길이를 나타내는 용어입니다.
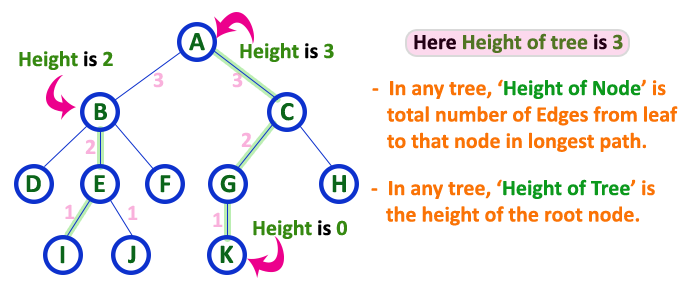
높이(Height) 는 트리에 존재하는 최대 경로 길이를 나타냅니다. 아래는 $I, J, K$ 노드에서 출발하여 루트 노드로 가는 경로의 길이가 최대이며 이 값이 3이므로 이 트리의 높이는 3이라고 할 수 있습니다.
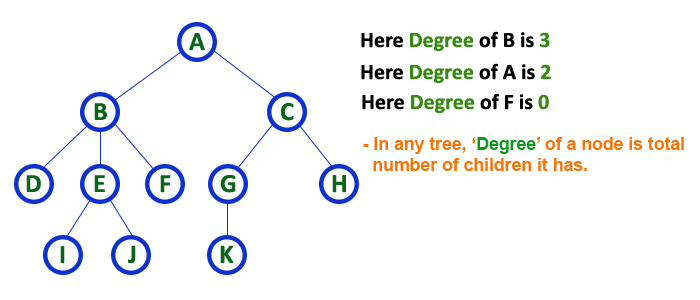
특정 노드가 가지고 잇는 자식 노드의 개수를 차수(Degree) 라고 하며 트리에 존재하는 모든 노드의 개수를 트리의 크기(Size) 라고 합니다. 위 이미지에 있는 트리는 총 11개의 노드를 가지고 있으므로 사이즈를 11이라 할 수 있습니다.
트리의 특징
트리에 존재하는 레퍼런스(엣지)의 개수는 노드 개수보다 하나가 적습니다. 루트를 제외한 모든 노드가 레퍼런스를 받기 때문에 레퍼런스 개수에 1을 더해주면 엣지의 개수가 됩니다.
특정 조건에서의 최대 노드 개수도 구할 수 있습니다. 최대 차수가 $d$ 인 트리에 대해서 깊이 $i$ 에서의 최대 노드 개수는 $d^i$ 입니다. 비슷하게 생각해보면 차수가 $d$ 이고 높이가 $h$ 인 트리에서 최대 리프 노드의 개수 역시 $d^h$ 로 나타낼 수 있습니다. 예를 들어, 차수가 $4$ 이고 높이가 $3$ 인 트리는 최대 $4^3 = 64$ 개의 리프 노드를 가질 수 있습니다.
등비수열 공식을 활용하면 최대 차수가 $d$ 이고 높이가 $h$ 인 트리의 최대 사이즈를 구할 수 있습니다. 각 깊이마다 최대 노드 갯수를 더해줍니다. 수식으로 나타내면 다음과 같습니다.
\[1+d+d^2+ \cdots + d^h = \frac{d^{h+1} - 1}{d - 1}\]
예를 들어, 차수가 $4$ 이고 높이 $3$ 인 트리는 최대 $\frac{4^{3+1} - 1}{4 - 1} = \frac{255}{3} = 85$ 개의 노드를 가질 수 있습니다.
특수한 트리들
특수하게 생긴 트리에 대해서는 특별한 이름을 붙여 부르기도 합니다. 아래 그림은 특수한 트리 구조를 이미지로 나타낸 것입니다. 이후 설명은 다음 노드를 가리키는 레퍼런스의 개수가 2인 이진 트리(Binary tree)를 기준으로 하겠습니다.

이미지 출처 : towardsdatascience.com
각 트리에 대해서 하나씩 알아봅시다. 먼저 Full Tree 는 모든 노드가 0 혹은 2개의 자식 노드를 가지는 트리입니다. 이진 트리의 경우 Full Tree의 리프 노드의 개수는 인터널 노드의 개수보다 하나 많습니다.
Complete Tree 는 왼쪽부터 차례대로 노드가 채워진 트리입니다. 이해를 돕기위해 이미지를 가져와 보겠습니다.

이미지 출처 : towardsdatascience.com
위 그림에서 왼쪽은 Complete Tree이고 오른쪽은 Complete Tree가 아닌 것들입니다. 오른쪽 맨 위에 있는 트리는 왜 Complete Tree가 아닐까요? 깊이가 2인 노드 중에서 가장 오른쪽 노드를 건너뛰고 깊이 3인 노드가 채워졌기 때문입니다. 그 왼쪽 아래에 있는 트리 역시 깊이 2인 노드 중에서 2번째 노드를 건너 뛴 채 3, 4번째 노드가 채워졌기 때문에 Complete Tree라고 할 수 없습니다. 오른쪽 아래에 있는 트리는 깊이가 3인 부분까지는 잘 채워졌지만 깊이 4인 노드를 채우면서 가장 왼쪽을 건너 뛰고 다음 노드를 채웠기 때문에 Complete Tree라고 할 수 없습니다.
다음은 Degenerate Tree 입니다. 이 트리는 리프 노드를 제외한 모든 노드가 1개의 자식 노드만을 가지고 있습니다. 이렇다보니 Degenerate Tree의 높이는 트리의 사이즈보다 하나가 작게 됩니다.
다음 Perfect Tree 는 모든 노드가 2개의 자식 노드를 가지며 모든 리프 노드가 동일한 깊이를 가지는 트리입니다. 높이가 $h$ 인 Perfect Tree는 높이 $h$ 인 트리의 최대 노드 개수이므로 위에서 등장했던 공식을 적용하여 Perfect Tree의 노드 개수를 $\frac{d^{h+1} - 1}{d - 1}$ 로 구할 수 있습니다.
마지막 Balanced Tree 입니다. 이 트리는 트리의 모든 노드에 대하여 왼쪽과 오른쪽의 하위 트리의 높이가 최대 1만큼씩만 다른 트리입니다. 이 또한 이해를 돕기 위해 이미지를 대동하겠습니다.

이미지 출처 : towardsdatascience.com
이 이미지의 왼쪽은 Balanced Tree를 만족하는 트리들이고 오른쪽은 Balanced Tree를 만족하지 않는 것들입니다. 오른쪽 맨 위에 있는 트리는 왜 Balanced Tree가 아닐까요? 깊이가 1인 두 노드 중에서 왼쪽 노드를 봅시다. 이 노드의 왼쪽 서브트리의 높이는 2입니다. 하지만 오른쪽에는 아예 노드가 존재하지 않기 때문에 오른쪽 서브트리의 높이는 0이 되어 두 트리의 높이 차이가 1이상이 됩니다. 그 아래 두 트리는 루트 왼쪽과 오른쪽 서브 트리의 높이 차이가 각각 3, 2 이기 때문에 역시 Balanced Tree가 아니게 됩니다.
To Binary Search Tree
연결된 리스트는 배열의 단점이었던 삽입과 삭제의 시간 복잡도를 해결했지만 탐색에 대해서는 여전히 최대 N번의 Operation을 필요로 했습니다. 트리는 연결된 리스트가 개선하지 못했던 탐색의 문제를 개선하기 위해 만들어진 자료구조 입니다. 다음에 등장하는 이진 탐색 트리(Binary Search Tree, BST) 는 탐색에 최적화된 트리 구조로, 데이터 탐색에 필요한 Operation의 개수를 훨씬 줄일 수 있습니다.
본 게시물은 문일철 교수님의 데이터 구조 및 분석을 참조하여 작성하였습니다.
Tree
이번 게시물에서 배울 자료구조는 트리(Tree) 입니다. 트리 구조 역시 배열(Array), 연결된 리스트(Linked List)와 동일하게 데이터를 저장하고 데이터간의 Operation을 표현하기 위한 추상화된 데이터 타입 중 하나입니다. 연결된 리스트를 변형한 것으로 연결된 리스트에서는 다른 노드를 가리키는 레퍼런스(Reference)가 하나뿐이었지만, 트리 구조에서는 여러 개의 레퍼런스를 가질 수 있습니다. 한 노드에서 시작해 여러 노드로 뻗어 나가는 모습이 나무를 거꾸로 뒤집은 모양과 유사하다고 하여 트리라는 이름이 붙었습니다.

이미지 출처 : 위키피디아 - 트리(자료구조)
트리 구조는 연결된 리스트의 일부를 변형시킨 것으로 연결된 리스트에서 가능했던 삽입(Insert), 삭제(Delete), 탐색(Search)이 모두 가능합니다. 또한 트리 구조에는 트래버스(Traverse)라는 새로운 작업이 있습니다.
트리 구조에서 사용되는 용어
트리 구조는 연결된 리스트보다는 훨씬 복잡합니다. 그렇기 때문에 트리의 복잡한 구조를 말로 나타내기 위한 다양한 용어들이 존재합니다. 트리 구조에서 사용되는 용어에 대해 아래 그림을 보며 알아봅시다.

이미지 출처 : tutorialspoint.com
가장 먼저 트리 최상단에 위치한 노드를 가리키는 용어는 루트(Root) 입니다. 그리고 직접 연결되어 있는 노드 중 상단에 위치한 노드를 부모(Parent) 노드라고 하고 아래에 위치한 노드를 자식(Child) 노드라고 합니다. 동일한 부모 노드로부터 나온 자식 노드는 서로 형제/자매(Siblings) 노드라고 합니다. 그리고 자식 노드를 갖지 않는 노드는 리프(Leaf) 노드라고 하며 다른 말로는 터미널(Terminal) 노드라고도 합니다. 리프 노드가 아닌 노드는 모두 인터널(Internal) 노드라고 합니다.
이미지 출처 : science.jrank.org
특정 노드에서부터 트리의 위쪽으로 거슬러 올라가면서 만나는 모든 노드를 조상(Ancestor) 노드라고 하며, 반대로 아래에 있는 모든 노드는 후손(Descendant) 노드라고 합니다.

이미지 출처 : btechsmartclass.com
특정 노드로부터 다른 노드로 갈 때 거치는 과정을 경로(Path) 라고 합니다. 경로 길이(Length) 는 출발 노드로부터 목적 노드까지 가는데 거치는 노드의 개수입니다. 위 이미지에서 제시한 두 예시의 경로 길이는 각각 $3, 2$ 가 됩니다. 그리고 깊이(Depth) 는 루트로부터 목적 노드까지의 경로 길이를 나타내는 용어입니다.

높이(Height) 는 트리에 존재하는 최대 경로 길이를 나타냅니다. 아래는 $I, J, K$ 노드에서 출발하여 루트 노드로 가는 경로의 길이가 최대이며 이 값이 3이므로 이 트리의 높이는 3이라고 할 수 있습니다.

특정 노드가 가지고 잇는 자식 노드의 개수를 차수(Degree) 라고 하며 트리에 존재하는 모든 노드의 개수를 트리의 크기(Size) 라고 합니다. 위 이미지에 있는 트리는 총 11개의 노드를 가지고 있으므로 사이즈를 11이라 할 수 있습니다.
트리의 특징
트리에 존재하는 레퍼런스(엣지)의 개수는 노드 개수보다 하나가 적습니다. 루트를 제외한 모든 노드가 레퍼런스를 받기 때문에 레퍼런스 개수에 1을 더해주면 엣지의 개수가 됩니다.
특정 조건에서의 최대 노드 개수도 구할 수 있습니다. 최대 차수가 $d$ 인 트리에 대해서 깊이 $i$ 에서의 최대 노드 개수는 $d^i$ 입니다. 비슷하게 생각해보면 차수가 $d$ 이고 높이가 $h$ 인 트리에서 최대 리프 노드의 개수 역시 $d^h$ 로 나타낼 수 있습니다. 예를 들어, 차수가 $4$ 이고 높이가 $3$ 인 트리는 최대 $4^3 = 64$ 개의 리프 노드를 가질 수 있습니다.
등비수열 공식을 활용하면 최대 차수가 $d$ 이고 높이가 $h$ 인 트리의 최대 사이즈를 구할 수 있습니다. 각 깊이마다 최대 노드 갯수를 더해줍니다. 수식으로 나타내면 다음과 같습니다.
\[1+d+d^2+ \cdots + d^h = \frac{d^{h+1} - 1}{d - 1}\]예를 들어, 차수가 $4$ 이고 높이 $3$ 인 트리는 최대 $\frac{4^{3+1} - 1}{4 - 1} = \frac{255}{3} = 85$ 개의 노드를 가질 수 있습니다.
특수한 트리들
특수하게 생긴 트리에 대해서는 특별한 이름을 붙여 부르기도 합니다. 아래 그림은 특수한 트리 구조를 이미지로 나타낸 것입니다. 이후 설명은 다음 노드를 가리키는 레퍼런스의 개수가 2인 이진 트리(Binary tree)를 기준으로 하겠습니다.

이미지 출처 : towardsdatascience.com
각 트리에 대해서 하나씩 알아봅시다. 먼저 Full Tree 는 모든 노드가 0 혹은 2개의 자식 노드를 가지는 트리입니다. 이진 트리의 경우 Full Tree의 리프 노드의 개수는 인터널 노드의 개수보다 하나 많습니다.
Complete Tree 는 왼쪽부터 차례대로 노드가 채워진 트리입니다. 이해를 돕기위해 이미지를 가져와 보겠습니다.

이미지 출처 : towardsdatascience.com
위 그림에서 왼쪽은 Complete Tree이고 오른쪽은 Complete Tree가 아닌 것들입니다. 오른쪽 맨 위에 있는 트리는 왜 Complete Tree가 아닐까요? 깊이가 2인 노드 중에서 가장 오른쪽 노드를 건너뛰고 깊이 3인 노드가 채워졌기 때문입니다. 그 왼쪽 아래에 있는 트리 역시 깊이 2인 노드 중에서 2번째 노드를 건너 뛴 채 3, 4번째 노드가 채워졌기 때문에 Complete Tree라고 할 수 없습니다. 오른쪽 아래에 있는 트리는 깊이가 3인 부분까지는 잘 채워졌지만 깊이 4인 노드를 채우면서 가장 왼쪽을 건너 뛰고 다음 노드를 채웠기 때문에 Complete Tree라고 할 수 없습니다.
다음은 Degenerate Tree 입니다. 이 트리는 리프 노드를 제외한 모든 노드가 1개의 자식 노드만을 가지고 있습니다. 이렇다보니 Degenerate Tree의 높이는 트리의 사이즈보다 하나가 작게 됩니다.
다음 Perfect Tree 는 모든 노드가 2개의 자식 노드를 가지며 모든 리프 노드가 동일한 깊이를 가지는 트리입니다. 높이가 $h$ 인 Perfect Tree는 높이 $h$ 인 트리의 최대 노드 개수이므로 위에서 등장했던 공식을 적용하여 Perfect Tree의 노드 개수를 $\frac{d^{h+1} - 1}{d - 1}$ 로 구할 수 있습니다.
마지막 Balanced Tree 입니다. 이 트리는 트리의 모든 노드에 대하여 왼쪽과 오른쪽의 하위 트리의 높이가 최대 1만큼씩만 다른 트리입니다. 이 또한 이해를 돕기 위해 이미지를 대동하겠습니다.

이미지 출처 : towardsdatascience.com
이 이미지의 왼쪽은 Balanced Tree를 만족하는 트리들이고 오른쪽은 Balanced Tree를 만족하지 않는 것들입니다. 오른쪽 맨 위에 있는 트리는 왜 Balanced Tree가 아닐까요? 깊이가 1인 두 노드 중에서 왼쪽 노드를 봅시다. 이 노드의 왼쪽 서브트리의 높이는 2입니다. 하지만 오른쪽에는 아예 노드가 존재하지 않기 때문에 오른쪽 서브트리의 높이는 0이 되어 두 트리의 높이 차이가 1이상이 됩니다. 그 아래 두 트리는 루트 왼쪽과 오른쪽 서브 트리의 높이 차이가 각각 3, 2 이기 때문에 역시 Balanced Tree가 아니게 됩니다.
To Binary Search Tree
연결된 리스트는 배열의 단점이었던 삽입과 삭제의 시간 복잡도를 해결했지만 탐색에 대해서는 여전히 최대 N번의 Operation을 필요로 했습니다. 트리는 연결된 리스트가 개선하지 못했던 탐색의 문제를 개선하기 위해 만들어진 자료구조 입니다. 다음에 등장하는 이진 탐색 트리(Binary Search Tree, BST) 는 탐색에 최적화된 트리 구조로, 데이터 탐색에 필요한 Operation의 개수를 훨씬 줄일 수 있습니다.

Comments